-
Calcula la esperanza matemática y la desviación típica de una variable aleatoria discreta de la que conocemos su tabla de distribución de probabilidad:
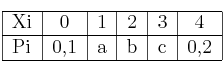
y además sabemos que ![P[X \leq 2] = 0,75 P[X \leq 2] = 0,75](local/cache-TeX/c45d8f65a43d2b75eef9c6b893713971.png) y que
y que ![P[X \geq 2] = 0,75 P[X \geq 2] = 0,75](local/cache-TeX/e104f3e0e6da5b2f6a3c142ac57120fb.png)
-
Un juego consiste en extraer una carta de una baraja española (40 cartas) y:
– si sale Sota o Saballo recibimos 15 céntimos
– si sale As o Rey recibimos 5 céntimos
– si sale cualquier otra carta pagamos 4 céntimos
Calcula la ganancia esperada.
-
Calcula los siguientes números combinatorios:
– 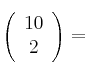
– 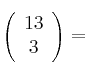
– 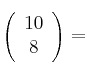
– 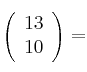
-
La probabilidad de que enceste un jugador de baloncesto es de 0,3. Si tira 5 tiros,
– a) ¿Cuál es la probabilidad de que enceste exactamente 2?
– b) ¿Y de que enceste al menos 4?
-
Una máquina produce 12 piezas defectuosas de cada 1000 que frabrica. Si analizamos 40 piezas producidas por dicha máquina, calcula:
– Probabilidad de que haya sólo pieza una defectuosa
– Probabilidad de que no encontrar ninguna pieza defectuosa