Ejercicios de Variables aleatorias unidimensionales. Binomial y Normal

(80) ejercicios de Variables Aleatorias Unidimensionales

(#2218) Seleccionar

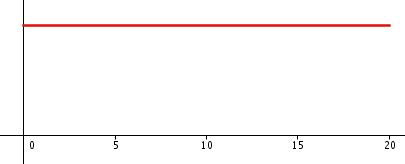
La siguiente imagen muestra la función de probabilidad (o densidad) de una variable aleatoria continua que anota el tiempo de espera de un tren que pasa cada 20 minutos. Calcula las probabilidades que se indican.

unidimensionales

– $P[X \leq 2]$
– $P[5 \leq X \leq 10]$
– $P[X \geq 10]$
(#2219) Seleccionar

Halla el valor de 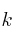$k$ para que la siguiente función sea una función de densidad

$f(x)= \left\{ \begin{array}{lcc} k & si & x \in [3,8] \\ \\0 & si & x \notin [3,8] \ \end{array} \right.$

Calcula las siguientes probabilidades:

– $P[2 < X \leq 5]$
– $P[X = 6]$
– $P[5 < X \leq 10]$
(#2220) Seleccionar

En una distribución Normal de media 110 y desviación típica 10, usa la gráfica (campana de Gauss) para calcular las siguientes probabilidades:

– $P[X \geq 110]$
– $P[110 < X < 120]$
– $P[110 < X < 130]$
(#2221) Seleccionar

En una distribución Normal de media 110 y desviación típica 10, usa la gráfica (campana de Gauss) para calcular las siguientes probabilidades:

– $P[120 < X < 130]$
– $P[X = 100]$
(#2225) Seleccionar

En una distribución normal 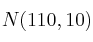$N(110,10)$ calcula $P[X \geq 110]$ de dos formas:

– Hallando el área bajo la función densidad
– Tipificando la variable

...
30
35
40
45
...

Crear un PDF con los Ejercicios Seleccionados