Ejercicios de Matemáticas Aplicadas a las Ciencias Sociales II (2º Bachillerato)

(37) ejercicios de Programación Lineal

(#4177) Seleccionar

a) Represente gráficamente la región determinada por las siguientes restricciones y determine sus vértices:
$2x+y \leq 6 \qquad 4x+y \leq 10 \qquad -x+y \leq 3 \qquad x \geq 0 \qquad y \geq 0$

b) Calcule el máximo de la función 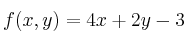$ f(x,y)=4x+2y-3$ en el recinto anterior e indique dónde se alcanza.
(#4193) Seleccionar

Dadas las siguientes restricciones:

$x \geq 0$
$y \geq 0$
$x+3y \leq 20$
$x+y \leq 10$

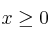
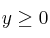
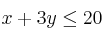
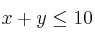
Representa la región limitada por dichas inecuaciones.
(#4194) Seleccionar

Dadas las siguientes restricciones:

$x \geq 0$
$y \geq 0$
$x+2y \leq 10$
$x \leq 2-y$

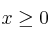
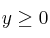
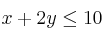
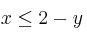
Encuentra los vértices de la región que representan las inecuaciones anteriores.
(#4195) Seleccionar

Dadas las siguientes restricciones:

$x \geq 0$
$y \geq 0$
$x+2y \leq 80$
$3x+2y \leq 120$

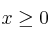
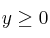
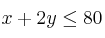
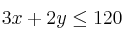
Encuentra en qué punto de la región limitada por las inecuaciones anteriores se hace máximo la función 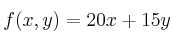$f(x,y)= 20x+15y$
(#4196) Seleccionar

Un pastor suministra a sus ovejas dos tipos de pienso con un contenido vitamínico por kilo como muestra la siguiente tabla. Ha de suministrarle diariamente al menos 5 mg de la vitamina A1 y 7 mg de la vitamina A2.

A1 A2

Pienso tipo 1 3 5

Pienso tipo 2 4 2

El precio del kilo de pienso del tipo 1 es de 0’5 euros, y el kilo de pienso del tipo 2 de 0’7 euros.

Si asignamos “x” al número de kilos de pienso de tipo 1 e “y” al número de kilos del pienso de tipo 2 que han de mezclarse para tener un coste mínimo, escribe las restricciones propias de este problema así como la función objetivo.

	A1	A2
Pienso tipo 1	3	5
Pienso tipo 2	4	2